Розрахунок конструкцій - Єврокод 3

 

Типи розрахунків 

Статичний розрахунок конструкцій, для визначення внутрішніх зусиль в елементах конструкції,  може бути виконаний із застосуванням декількох типів розрахунку:

• лінійно-пружний розрахунок першого порядку

Використовується вихідна геометрія конструкції та розглядається лінійна поведінка матеріалу. Тобто, геометрія розрахункової схеми залишається незмінною при виконанні статичного розрахунку, а напруга у елементах конструкції не перевищує межу текучості (залежність між напругою у матеріалі та її деформаціями має лінійний характер).

• лінійно-пружний розрахунок другого порядку

Використовується змінна геометрія конструкції і розглядається лінійна поведінка матеріалу. Змінну геометрію доводиться враховувати у разі, коли незначні відхилення від початкової геометрії призводять до суттєвого впливу на внутрішні зусилля в елементах конструкції. Причина полягає в тому, що розрахункова схема – це по суті ідеалізоване уявлення конструктивної (реальної) схеми. Суто вертикальні елементи в розрахунковій схемі насправді можуть бути дещо відхилені від вертикалі; передача навантаження від одного елемента до іншого (внаслідок технологічного монтажу) виконується з деяким додатковим ексцентриситетом.

Ці деформації, що викликані недосконалостями геометрії, впливають на внутрішні зусилля. Розрізняють недосконалості: загальні (для рам і в’язевих елементів) та місцеві (для окремих елементів).

Відхилення (Δ)  від початкової геометрії, що викликані загальними недосконалостями називають P-Δ ефект.

  В результаті осьового стискання елементи згинаються в поздовжньому напрямку. Це призводить до зниження згинальної жорсткості окремого елемента. Така місцева недосконалість називається P-δ ефект.

На рисунку нижче показані відмінності розрахунків першого і другого порядку.

• пружно-пластичний розрахунок першого порядку

Використовується вихідна геометрія та розглядається нелінійна поведінка матеріалу. У цьому типі розрахунку враховується факт перевищення межі текучості у матеріалі. У цьому випадку в елементах конструкції розвиваються пластичні деформації, утворюються пластичні шарніри, що впливають на розрахункову схему. Деякі елементи конструкції можуть бути виключені з розрахункової схеми. Такий розрахунок визначають як нелінійний.

• пружно-пластичний розрахунок другого порядку

Використовується змінна геометрія і розглядається нелінійна поведінка матеріалу. Це нелінійний розрахунок.

 

Визначення порядку розрахунку 

        Для визначення порядку розрахунку розраховують коефіцієнт стійкості: 

   α_cr  визначає  - у скількі разів треба збільшити діюче навантаження F_Ed для отримання втрати стійкості конструкції у пружній стадії, що викликано пружним критичним навантаженням F_cr.

Розрахунок першого порядку виконується у разі дотримання умови:

α_cr ≥ 10 для пружного аналізу

α_cr ≥ 15  для пластичного аналізу

Отримання значення F_cr  вручну достатньо складне і пов’язане із визначенням форм коливань конструкції. Тому, для розрахунку F_cr зазвичай використовують сучасне програмне забезпечення.

Існує дещо спрощений підхід. Для рамних конструкцій, у якості альтернативи автоматизованому розрахунку, α_cr  визначається на підставі геометрії рами, прикладеного навантаження і горизонтальних деформацій:

             де

H_Ed– розрахункове значення горизонтальної реакції у нижній частині поверху від горизонтальних навантажень і фіктивних горизонтальних навантажень;

V_Ed – сумарне розрахункове вертикальне навантаження на конструкцію у нижній частині поверху;

δ_H,Ed– горизонтальне переміщення верхньої частини поверху відносно нижньої частини;

h – висота поверху.

Рис. Навантаження та горизонтальне переміщення поверху

 

Для багатоповерхових каркасів α_cr визначається для кожного поверху. Хоча найчастіше висновок можна зробити на основі аналізу нижнього поверху конструкції.

Як бачимо, горизонтальне навантаження H_Ed включає фіктивне горизонтальне навантаження. Останнє визначається за певними правилами залежно від вертикального навантаження V_Ed.  Це означає обов’язкову наявність горизонтального навантаження навіть при відсутності фактичного горизонтального навантаження. Прикладання фіктивного навантаження і дозволяє врахувати можливі геометричні недосконалості.

 Для каркасів будівель: геометричними недосконалостями другого порядку можна знехтувати при виконанні нерівності:

H_Ed ≥ 0.15 V_Ed

Така ситуація можлива за умови діючого (значного за величиною) горизонтального навантаження.

 

Врахування ефектів другого порядку 

Для одноповерхових та багатоповерхових рам (за умови, що усі поверхи мають однаковий: розподіл вертикальних і горизонтальних навантажень; та жорсткості рами по відношенню до по­перечних сил, прикладених до поверхів) -  ефекти другого порядку можуть бути враховні шляхом збільшення гори­зонтальних навантажень H_Еd на коефіцієнт 1/(1 – 1/α_cr): 

Розрахунок фіктивного горизонтального навантаження

 

Наявність початкових недосконалостей рами реалізується впровадженням системи еквівалентних горизонтальних фіктивних сил. Для цього, діючі вертикальні сили V_Ed домножуються на коефіцієнт φ. Він залежить від базового значення φ₀, висоти конструкції та кількості тримальних колон:

φ₀= 1/200;

α_h- понижуючий коефіцієнт для висоти h, що застосовується до колон

  але  

h - висота конструкції в м;

         α_m  – понижуючий коефіцієнт, що враховує кількість колон у ряду; 

Приклад оцінки недосконалості рамної конструкції

 

В цьому прикладі з’ясовується необхідність врахування ефектів другого порядку при розрахунку рамної конструкції.

Вихідні дані.

Рис. Розрахункова схема рами с горизонтальним навантаженням

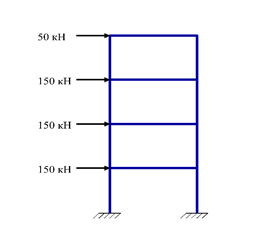
Рис. Розрахункова схема з вертикальним навантаженням 

Діючі вертикальні сили домножуються на коефіцієнт φ

α_h - понижуючий коефіцієнт для висоти h, що застосовується до колон

 

де h=4.5 м - висота поверху; 

α_m  – понижуючий коефіцієнт, що враховує кількість колон у ряду    

Фіктивні горизонтальні сили на рівні поверхів:

H₄ = 500 ˙ 0.004 = 2 кН

H_3-1 = 1500 ˙ 0.004 = 6 кН 

Рис. Розрахункова схема рами с горизонтальним фіктивними силами

Попередня перевірка:

геометричними недосконалостями другого порядку можна знехтувати при виконанні нерівності якщо  H_Ed ≥ 0.15 V_Ed

 Маємо

H_Ed = 2˙2 + 6˙6 + 50 +150˙4 = 690 кН

V_Ed = 500˙2 + 1500˙6 = 10000 кН

690 ≤ 0.15 ˙ 10000 = 1500

Висновок: попередня умова не виконується. Необхідно враховувати ефекти другого порядку.

Горизонтальне навантаження розрахуємо із застосуванням коефіцієнта стійкості α_cr за допомогою наближеної формули:

 Горизонтальне переміщення рамної конструкції δ_H,Ed  (від горизонтальних та фіктивних сил) отримаємо на підставі статичного розрахунку у пружній стадії за допомогою будь-якого програмного забезпечення, наприклад

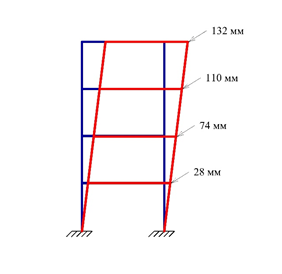
Рис. Горизонтальне переміщення рами в мм

Згідно отриманого результату визначаємо горизонтальне переміщення верхньої частини поверху відносно нижньої частини поверху:

Для 4 поверху

Для 3 поверху

Для 2 поверху 

Для 1 поверху

Розрахунок другого порядку необхідно виконувати якщо  α_cr  < 10 .

Остаточний висновок: треба враховувати розрахунок другого порядку.

Ефекти другого порядку від поперечного зміщення, спричинені вертикальними навантаженнями, можуть бути обчислені шляхом збільшення гори­зонтальних навантажень згідно з теорією першого порядку за допомогою коефіцієнта (за умови, що α_cr ≥ 3,0):

Таким чином, сумарне горизонтальне навантаження с урахуванням коефіцієнту 1.23 повинно бути:

Рис. Розрахункова схема рами с горизонтальними силами

 

Розрахунок із використанням програмного забезпечення Robot Structural Analysis 

Розглядається розрахункова схема, що була надана вище. Наприклад,

Визначення коефіцієнта стійкості  α_cr для конструкції 

В меню програми змінимо тип розрахунку Analysis->Analysis Types … після натискання на кнопку Change analysis type.  В діалозі змінено тип на Buckling

 Після підтвердження, в діалозі, призначимо число форм коливань, наприклад

 Необхідний результат - коефіцієнт стійкості  α_cr - отримуємо із Results->Advanced->Critical loads

            Мінімальне значення коефіцієнту α_cr = 6.13 вказує, що розрахунок другого порядку є необхідним.

   

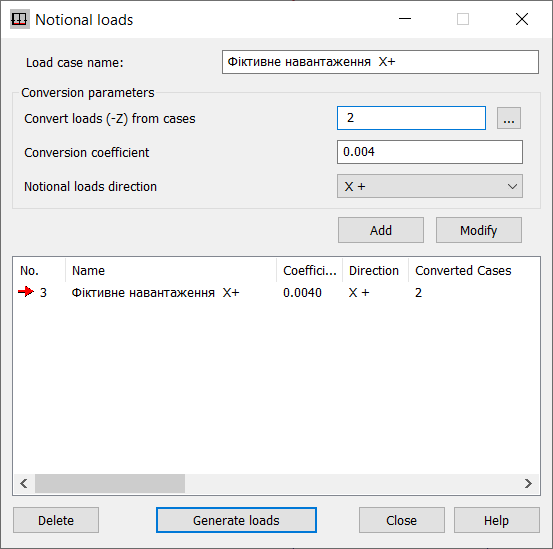
Визначення фіктивного горизонтального навантаження

 Для отримання фіктивного горизонтального навантаження задіємо інструмент програми, що перераховує вертикальне навантаження у горизонтальне  за допомогою коефіцієнта  φ=0.004 (див. ручний розрахунок вище). Функція викликається в меню програми Loads->Special Loads->Notional loads

Після клацання на кнопці Genegate loads отримуємо результат:

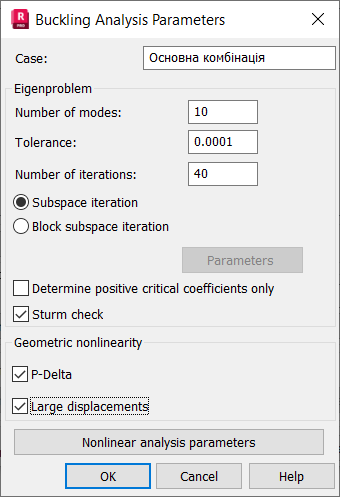
            Із отриманих дій, створимо необхідні комбінації. Для розрахункової комбінації призначимо тип розрахунку Buckling. Для параметрів за замовчуванням додамо включення флагів Р-Delta та Large displacements. Активація флагів дозволяє розраховувати внутрішні зусилля в елементах конструкції з урахуванням геометричної нелінійності.

Рис. Вид вікна для налаштування параметрів розрахунку

Включення флага Р-Delta автоматично збільшує внутрішні зусилля на коефіцієнт 1/(1 – 1/α_cr).

.